| Navigation | Equipment | Culbertson | White Cliffs | Great Falls | Gates of the Mountains | Three Forks | Beaverhead Rock | Pompeys Pillar | Terry |
Lewis and Clark in Montana — a geologic perspective
Navigation — finding the latitude
Three Forks of the Missouri, July 27, 1805:
. . . beleiving this to be an essential point in the geography if this western part of the Continent I determined to remain at all events untill I had obtained the necessary data for fixing it's latitude Longitude &c.
Until the latter part of the 20th Century, the most common observational method to find one’s latitude was to use a sextant or octant and take a noon shot of the sun. The noon shot was preferred because 1) an accurate timepiece was not necessary and 2) an observation taken when the sun is due north or south (that is, on the observer’s meridian) greatly simplifies the calculations (see Part II, below).
Let’s use Lewis’s observation at the Three Forks to show how the captains made their observations and calculations to determine latitude.
Part I, Using the Octant to take the observation
When the sun’s noon altitude was greater than 60° (April - September) Lewis and Clark used their octant, which was equipped for the back-sight method (see Equipment). Using the back-sight method, their octant theoretically could measure an angle between two objects up to 180°.
 |
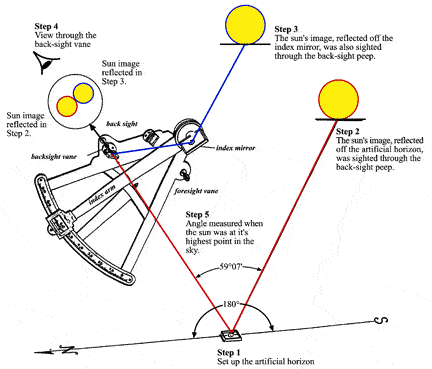| Taking a noon observation with the octant and artificial horizon by the "back" method. |
- Shortly before noon on July 29, 1805. Lewis prepares to take an observation of the sun for latitude. Because mountains to the south rise above the natural horizon, Lewis prepares an artificial horizon using a tray filled with water; the water will form a level surface and reflect the sun’s image to his eye.
- Lewis places his eye to the octant’s back-sight vane. He then looks through a slit in the back-sight horizon glass and finds the image of the sun reflected from the water in the tray.
- While still sighting the sun’s image reflected from the water, Lewis moves the octant’s index arm with its index mirror until the sun’s image is reflected from the index mirror to the back-sight horizon mirror and then to his eye. Because Lewis wants to obtain the altitude of the sun’s lower limb he brings the two images together so that the bottom of the sun’s image reflected from the index mirror just touches the top of the sun’s image reflected from the water.
- As the sun continues to move toward its highest point in the sky for the day (noon), the two images of the sun overlap. To keep the two images in contact at a single point, Lewis turns the tangent screw on the octant’s index arm, gradually decreasing the angle measured by the index arm.
- Lewis keeps the two images just touching each other. When the two images stop overlapping, Lewis knows that the sun has reached it highest point in the sky. The images remain just touching each other for ten seconds or so, then begin to separate as the sun slowly descends. Lewis, however, already has clamped the index arm in place and, with the help of the vernier, reads the angle on the graduated arc as indicated by the zero mark on the index arm. That angle is 59°07'.
The angle that Lewis measured during this noon shot is not the altitude of the sun’s center but: 180° minus 2x the altitude of the sun’s lower limb. The angle he measured also includes angles caused by mirror misalignment (index error), refraction (see Step D), parallax (see Step E), sun’s semidiameter (the angle between the sun’s lower limb and its center — see Step F) and the sun’s declination (angular distance north or south of the equator — see Step G). All these angles have to be eliminated in order to derive the true altitude of the sun’s center with respect to the earth’s center.
The first step in making corrections to the observed angle usually is to subtract the index error (or in some manuals, apply index correction) but . . .
A) Lewis first divides the angle he measured by 2
| 59°07'> |
| ÷ 2 < |
| 29°33'30" |
Because Lewis had to measure the angle between the ray reflected from the index mirror and that from the artificial horizon, the observed angle is twice that from a natural horizon alone.
B) Then he subtracts the result of Step A from 90°
| 90°00'00" |
| - 29°33'30" |
| 60°26'30" |
Since Lewis already has divided the observed angle by 2 in Step A, he must subtract that result from 90°, not 180°.
C) Next Lewis adds half the OCTANT’S INDEX ERROR
Lewis, in his journal for July 22,
1804, recorded that the octant’s index error in the “back-method” was
+2°11'40.3". The octant’s index error actually was +4°23'20.6";
that is, it read too high by that amount. Lewis, however, began
his corrections by dividing his measured angle by 2 and, thus needed to
apply only half the index error (though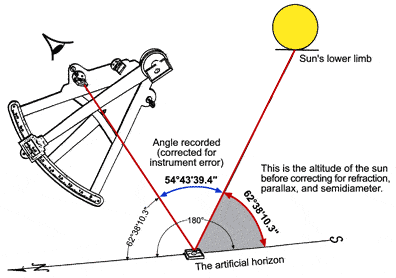 
still calling it “index error”).
Because Lewis’s octant read high, the index error should be subtracted,
but owing to the sequence Lewis used to make his corrections, he needs
to add 2°11'40.3" to the result of Step B.
| 60°26'30" | |
| + 2°11'40.3" | |
| 62°38'10.3" = 62°38'10" =apparent altitude of | |
| sun’s lower limb | |
Note: Although the octant’s index error by Lewis’s method was +2°11'40.3", he mistakenly used an index error of +2°40" throughout 1805. He discovered this mistake while at Fort Clatsop on the Pacific Coast. Using the wrong index error made the latitude he calculated on July 29 too far south by about 0°28'20" or about 32½ miles. The calculations here are made as if he had used the correct index error. |
|
D) Then he makes the correction for REFRACTION
| 62°38'10" apparent altitude of sun’s lower limb |
| - 0°00'24" refraction correction |
| 62°37'46" apparent altitude of sun’s lower limb corrected for refraction |
Lewis opens his book Tables Requisite to the table “Mean Refraction” and, using the altitude derived from Step C, he finds that he has to subtract 24".
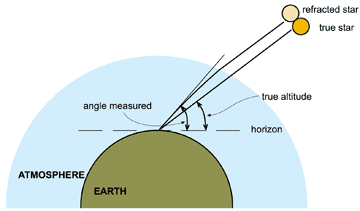
Refraction is the bending of a light ray as it passes through the atmosphere. This bending results from the increase in the atmosphere’s density as the light ray travels downward toward the observer.
Refraction makes an object appear higher in the sky than it actually is.
The light ray always appears to be bent upwards except when it is vertical, therefore, Lewis subtracted 24" from the apparent altitude found in Step C.
E) Lewis then makes the correction for PARALLAX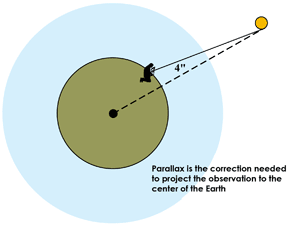
The latitude that Lewis is calculating must be measured from the center of the earth. Lewis again goes to his Tables Requisite, opens it to the table “Parallax of the Sun in Altitude”, and, using the apparent altitude of the sun’s lower limb from Step C, finds that he has to add 4".
| 62°37'46" altitude of lower limb corrected for refraction | |
| + 0°00'04" parallax correction | |
| 62°37'50" sun’s lower limb projected to the center of the earth |
F) . . . adds the SUN’S SEMIDIAMETER
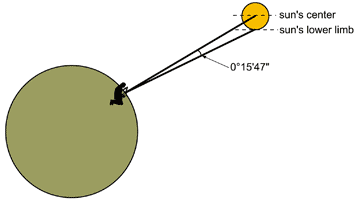It
is usually easier for an observer to find either the upper or lower limb
of the sun rather than its center. Lewis, when using the octant, always
shot the sun’s lower limb. The angular difference between the sun’s
center and its upper or lower limb is called its “semidiameter” (half
diameter). The Nautical Almanac Lewis used had a table giving the sun’s
semidiameter at Greenwich noon for the 1st, 7th, 13th, 19th and 25th of
each month. For July 25, 1805 it was 15'46.7" and on August 1 it was
15'47.5" For his observation on July 29, Lewis determines a semidiameter
of 15'47". He adds this to the result of Step E to find the true altitude’s lower limb.
| 62°37'50" altitude of lower limb projected to the center of the earth | |
| + 0°15'47" sun’s semidiameter | |
| 62°53'37" true altitude of the sun with respect to the earth’s center |
G) . . . and subtracts the SUN’S DECLINATION
Now Lewis has the true altitude of the sun’s center above the horizon, but that altitude includes the sun’s north declination.
A celestial body’s declination is the number of degrees that body is north or south of the celestial equator at a given moment as “viewed” from the center of the earth. The declination of stars and distant planets changes slowly, but the sun’s declination changes by more than 23° between the equinoxes, stopping only for a brief interval at the solstices. From the spring equinox until the autumnal equinox the sun’s declination is North (+); the remainder of the year its declination is South (-).
The angle that Lewis has just measured includes the sun’s North declination. Therefore, he must subtract the sun’s declination from the result of Step F. If the declination had been south he would add it.
The Nautical Almanac for 1805 that Lewis carried,
however, gave the sun’s declination only for noon of each day at
Greenwich, England. Lewis, thus, has to determine what the sun’s
changing declination would have been at the time of his observation. To
do this he has to make a separate set of calculations.
How did Lewis determine the sun’s declination at the time of his observation? |
|||||||||||||
| a) Lewis looks in his Nautical Almanac for July. On page 74 in the column with the heading “Day of the Month” he finds 29 and | |||||||||||||
| following across to the right to the column with the heading “Declin. North” he finds ................. | 18°50'01" (July 29) | ||||||||||||
| and for the 30th he finds ............................................................................................................... | -18°35'44" (July 30) | ||||||||||||
| b) He subtracts the declination for July 30 from that for July 29 | 0°14'17"change per day | ||||||||||||
| c) Then he divides that result by 24 to find the change in sun’s declination per hour | ÷ 24 | ||||||||||||
| °0'35.7"change per hour | |||||||||||||
d) Now Lewis needs to know how many hours had elapsed
between noon at Greenwich and noon at the Three Forks. The number of hours
elapsed multiplied with the hourly rate gives the total change in declination
since Greenwich noon. Lewis finds the number of hours elapsed by dividing
his longitude by 15. He doesn’t know his exact longitude, but he
can estimate it or derive it by dead-reckoning. Lewis didn’t save
his calculations, so let’s assume he used 111° West as his longitude:
Therefore since Greenwich noon July 29 the sun’s °04'24". e) Lewis subtracts this amount from the sun’s noon declination
Finally, he subtracts the sun’s declination from the result of Step F |
|||||||||||||
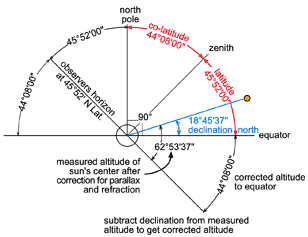
H) From co-latitude to latitude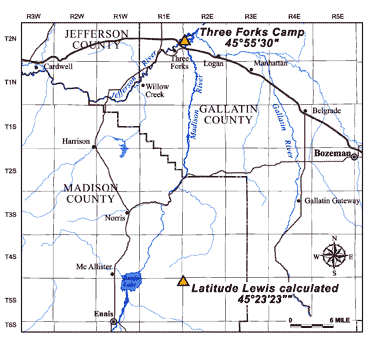
Steps A through G produce what is called
a “co-latitude”.
A co-latitude is the angle which, when added to the latitude equals
90°; that is
90° - co-latitude = latitude.
To derive the calculated latitude from this observation Lewis subtracts the co-latitude from 90°
| 90°00'00" | |
| - 44°08'00" | |
| 45°52'00" | LATITUDE |
| 45°52' | Latitude to nearest arc minute per this observation (about 3 miles too far south) |
| 45°55½' | Latitude of camp determined from map analysis |
| 45°23'23" | Lewis’s calculated latitude using incorrect
index error of 2°40' instead of 2°11'40" |
